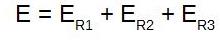En esta publicación les comentaré sobre los circuitos eléctricos, que son la base principal de cualquier equipo eléctrico y electrónico, ya que estos no son mas que un grupo de circuitos, así que comencemos.
La
electricidad es la base de todo, tal como dije en una publicación anterior.
Asimismo todo el avance tecnológico actual se basa en circuitos
eléctricos, siendo un circuito eléctrico
el recorrido que hace una corriente eléctrica, y cuyos elementos son:
- · Fuente de energía
- · Corriente eléctrica
- · Resistencia o carga
Los
elementos de un circuito eléctrico se relacionan a través de la ley de Ohm, que
es sino la principal una de las principales leyes de la electricidad, que dice
así:
De
acuerdo a como está conformado, un circuito eléctrico puede ser de los
siguientes tipos:
- · Serie
- · Paralelo
- · Serie-paralelo
Cada
uno de ellos tiene sus características, de las cuales voy a explicar en esta
publicación, tratando de hacerlo desde un punto de vista práctico, es decir,
que se vea en algo que usamos de forma cotidiana, pero que muchas veces no nos
damos cuenta. Comencemos entonces con los circuitos en serie.
Circuitos en
serie
En
este tipo de circuitos, los elementos que lo conforman están conectados uno a
continuación del otro, tal como se muestra en la figura.
La
principal característica de los circuitos en serie es que la corriente que
circula por el mismo es la misma para cada uno de sus elementos. Por ejemplo,
si en un circuito hay tres resistencias conectadas en serie, la corriente que
pasa por cada una de ellas será la misma.
Se
tiene también que en un circuito en serie, al pasar una corriente por las
diferentes cargas que están conectadas al mismo, habrá una diferencia de
potencial o tensión en los extremos de las mismas. Si se suman las tensiones presentes en las cargas o
resistencias del circuito, el resultado será igual al valor de la tensión de
fuente de energía que alimenta al circuito, la cual se puede calcular por la
ley de Ohm.
Por
último la suma de las potencias en cada una de las cargas es igual al valor de
la potencia total del circuito. Dichas potencias se calculan por la ley de
Joule.
Circuitos en
paralelo
En
este tipo de circuitos, los elementos que lo conforman están conectados uno al
lado del otro, tal como se muestra en la figura.
La
principal característica de los circuitos en paralelo es que la tensión o
diferencia de potencial es la misma para cada uno de sus elementos. Por
ejemplo, si en un circuito hay tres resistencias conectadas en paralelo, la
tensión en cada una de ellas será la misma.
Se
tiene también que en un circuito en paralelo, pasará una corriente por las
diferentes cargas que están conectadas al mismo, cuyo valor dependerá del valor
de cada carga y las cuales se pueden calcular por la ley de Ohm. Si se
suman las corrientes presentes en las
cargas o resistencias del circuito, el resultado será igual al valor de la
corriente total o principal que circula por el circuito
Circuitos mixtos
o serie-paralelo
Este
tipo de circuitos es una mezcla de circuitos en serie y en paralelo, tal como
se muestra en la figura.
Para
calcular los diferentes valores de corriente y tensión, se aplica la ley de
Ohm, tomando en cuenta las partes del circuito que están ya sea en serie o en
paralelo. Al
igual que en los circuitos en serie y en paralelo, en los circuitos mixtos la
suma de las potencias en cada una de las cargas es igual al valor de la
potencia total del circuito, las cuales se calculan por la ley de Joule
