Aplicación de las cónicas. Parábolas y su uso en las comunicaciones

Saludos. Esta vez vengo con la intención de responder aquella pregunta que dice así: ¿para que sirven las matemáticas? Pues bien, en este caso vamos a ver un uso practico de ellas, específicamente en las comunicaciones y mas exactamente del uso de las cónicas en especial las parábolas, pues entonces comencemos.

. 

Las cónicas son usadas actualmente en tecnología, pero antes de ver como se aplican haremos un repaso de algunos conceptos.

¿Qué son cónicas?

Las cónicas o secciones cónicas son curvas planas obtenidas mediante la intersección de un cono con un plano, de allí el nombre. De acuerdo al ángulo en que el plano corte al cono se tendrá los distintos tipos de cónicas, los cuales son:

• Circunferencia
• Elipse
• Parábola
• Hipérbola

En la siguiente imagen se muestran los distintos tipos de cónicas:

Cónicas 

Vamos a analizar las parábolas que son las usadas en las telecomunicaciones.

¿Qué es una parábola?

Una parábola es una cónica obtenida del corte de un plano en ángulo oblicuo a un cono. Más exactamente una parábola es una curva en la que los puntos están a la misma distancia de una recta fija y de un punto fijo. La recta fija es llamada directriz y el punto fijo es llamado foco. 

Parábola

La directriz es perpendicular a otra recta llamada eje en la cual está ubicado el foco, indicado por F y la distancia, que se indica por P, que hay del foco al vértice, indicado por O, es la misma que hay del vértice a la directriz, indicada por D, asimismo, por el foco pasa una recta perpendicular al eje que es llamada lado recto, indicada por la letra L, y que corta a la parábola en dos puntos. En la imagen se muestra como esta compuesta una parábola.

Como esta compuesta una parábola

Ahora bien, supongamos que el vértice O está en el origen del eje de coordenadas y que la directriz corta al eje en un punto –X, mientras que el foco es un punto P en el eje X, por lo que sus coordenadas serán (P,0), la fórmula de una parábola es:

Y² = 4PX

Ecuación de la parábola

Si la parábola tuviese su directriz perpendicular al eje Y, es decir, abriría en forma vertical, y siguiendo el razonamiento anterior, su fórmula sería:

Ecuación de la parábola vertical

Conocemos lo que es una parábola y su forma ¿Pero qué aplicación práctica le podemos encontrar a esta cónica? Pues bien, las parábolas las vemos muy a menudo, y en caso que no sea así, hacemos uso de ella hasta sin darnos cuenta, como es el caso de las antenas parabólicas, que tal como su nombre lo indica, su forma proviene de una parábola. Vemos cantidad de antenas parabólicas usadas principalmente para recibir señales de televisión por satélite, pero sirven para otras aplicaciones como telefonía, comunicaciones y en astronomía, los llamados radiotelescopios son grandes antenas parabólicas.

Antenas parabólicas

Una de las propiedades más utilizadas de las parábolas es la de reflexión, la cual consiste en lo siguiente: un rayo que sale del foco se refleja sobre la superficie de la parábola saliendo de forma paralela a su eje y un rayo que llegue de forma paralelo al eje de la parábola, se refleja en ella dirigiéndose al foco. Las antenas parabólicas funcionan con este principio cuando un flujo de ondas electromagnéticas choca contra su superficie, reflejándose en el foco de la parábola.

Propiedad de reflexión de las parábolas

Para diseñar una antena parabólica se usan los conceptos vistos anteriormente. Si la parábola abre en forma vertical, su ecuación es:

X² = 4PY

Si el vértice de la parábola está en el origen del eje de coordenadas, es decir, está en el punto (0,0) y el foco está ubicado en un punto P en el eje Y, por lo que sus coordenadas serán (0, P). Ahora vamos a ver los elementos de una antena parabólica y como se calculan, tal como se muestra en la siguiente figura:

Elementos de una antena parabólica

Si ahora la parábola abre en forma horizontal, su ecuación es:

Y² = 4PX

Si se asume que el vértice de la parábola está en el origen del eje de coordenadas, es decir, en el punto (0,0) y el foco está ubicado en un punto P en el eje X, por lo que sus coordenadas serán (P, 0). Los elementos de una antena parabólica y como se calculan para este caso, es de forma similar si la parábola abriera en forma vertical, tal como se muestra en la siguiente figura:

Elementos de una antena parabólica si abre horizontalmente

Hagamos un ejemplo práctico: para una antena de 6 metros de diámetro y un foco de 2 metros, calcular la profundidad y el ángulo de abertura.

Sea P el foco, D el diámetro y H la profundidad, entonces si:

D: 6 metros

P: 2 metros

Para determinar estos valores se hace lo siguiente:

Ejemplo de antena parabólica

Para que la antena obtenga su forma a la parábola se le hace girar sobre su eje:

Giro de una parábola

Para hallar el volumen de la misma, se calcula por integrales por el método de solido de revolución, el cual es igual a:

Volumen de una antena parabólica

Si la parábola abre de forma horizontal, esto se calcula así:

Volumen de una antena parabólica que abre horizontalmente

Ahora calcularemos el volumen que ocupará la antena del ejemplo anterior, para lo cual usaremos integración definida:

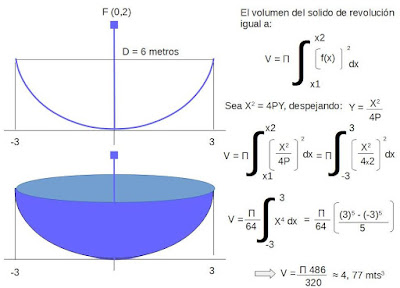Ejemplo del calculo del volumen de una parábola 

Vamos a dejarlo hasta aquí. Este teme es mas extenso y quise mostrar solo un resumen del mismo, el cual espero les haya gustado. Pueden hacer cualquier comentario o sugerencia y no olviden suscribirse a este blog. ¡Hasta la próxima!