Que es el número áureo o numero phi

Saludos. En esta ocasión les relataré sobre el número áureo o número phi, el cual es uno de los mas importantes y el cual está presente hasta en la naturaleza. Sin mas nada, comencemos.

¿Que se conoce como número áureo o phi?

El número áureo, número de oro, “divina proporción”, “proporción de oro” (se pronuncia fi) es una cifra producto de una relación o proporción (tal como el número pi que es la relación entre la longitud de una circunferencia y su diámetro) y fue descubierto en la antigüedad al ser observada la proporción presente en figuras geométricas, siendo dicha relación o proporción un valor constante. Este número también es llamado phi (se pronuncia fi) y su símbolo la letra griega del mismo nombre (Φ), esto fue en homenaje al escultor griego Fidias, quien vivió en el siglo V A. C. y quien aplicaba esta cifra en sus obras, por ser esta es la primera letra de su nombre, siendo el ingeniero y matemático estadounidense Mark Barr quien empezó a usar dicha notación en el año 1909, mientras que el nombre de número áureo o de oro es atribuido al gran artista e inventor italiano Leonardo Da Vinci.

¿Pero puede ser cualquier proporción la que de como resultado ese valor constante?

No, no puede ser cualquier proporción o relación, sino una como la descrita por el gran matemático griego Euclides, quien en el libro 6 de su obra “Los elementos” expone lo siguiente:

“Se dice que una recta ha sido cortada en extrema y media razón cuando la recta entera es al segmento mayor como el segmento mayor es al segmento menor.”

Esto sería así: Se tiene una recta L que se divide en dos segmentos llamados a y b:

A partir de esta recta se determina el numero phi

Entonces, la relación entre la recta L, que es igual a la suma de los segmentos a y b, o sea L = a+b, y el segmento a debe ser la misma que la relación entre el segmento a y el segmento b. Cuando esta relación se cumple, se dice que los segmentos a y b están en proporción áurea:

Proporción áurea

Valor del número áureo o número phi

¿Pero cual sera el valor de dicha proporción? Para saberlo, supongamos que los segmentos a y b en los que se dividió la recta L miden X y 1 respectivamente:

a= X

b=1

Se sustituyen valores, es decir donde está a se coloca X y donde está b se coloca 1, y se hacen los cálculos correspondientes, tal como se muestra en la figura:

Como se calcula el valor del número phi

Como estamos hablando de longitudes, se toma la solución negativa, entonces El número áureo, número de oro, “divina proporción”, “proporción de oro” o número phi (Φ) es igual a :

Valor del numero phi

 Con lo anterior, se observa también que el número phi es un número irracional, ya que no se puede representar como la fracción de dos enteros.

Si ahora en a en vez de X colocamos el valor de Φ, mientras que b sigue valiendo, tendremos lo siguiente:

Propiedad del número phi

Se obtiene la misma cifra a ambos lados de la igualdad, lo que indica que se tiene igual proporción. Asimismo, esto nos indica que el numero phi se puede escribir también en términos de si mismo:

Otra propiedad del número phi

Mas específicamente, siempre se cumplirá que:

Otra propiedad del número phi

El numero áureo también se puede determinar mediante fracciones continuas y por raíces anidadas

Otra forma de calcular el valor del número phi

El numero phi cuenta con una enorme cantidad de decimales, llegándose en el año 2000 a calcularle billón y medio.

Propiedades del número phi

El número áureo o número phi tiene las siguientes particularidades que lo hacen único:

El número phi ( Φ) elevado al cuadrado es igual a la suma de este mas 1:

Número phi al cuadrado

El número phi ( Φ) menos 1 es igual a su inverso:

Inverso del número phi

 El número phi ( Φ) elevado al cubo es igual a:

  

Número phi al cubo

 Asimismo se tiene que:

Potencia del número phi

El rectángulo áureo

Una aplicación de este número especial es en el llamado rectángulo áureo, el cual es un rectángulo en el que la proporción entre sus lados es igual al número áureo. Es llamado así ya que por sus proporciones resulta ser agradable a la vista, siendo conocido por los antiguos griegos que lo usaban para diseñar sus templos y edificios. Este rectángulo se crea de la siguiente manera: se tiene un cuadrado al cual se le marca el punto medio de uno de sus lados. Este punto se une con uno de los vértices del lado opuesto con una recta y se lleva dicha recta sobre el lado inicial, obteniéndose el lado mayor del rectángulo. Si se divide la distancia del lado mayor con la distancia del lado menor, se tendrá como resultado el numero phi.

Rectángulo áureo

Para demostrar lo anterior, se hará un ejemplo para un cuadrado cuyos lados miden 6 centímetros, para lo cual se traza una recta que va desde el punto medio de uno de sus lados hasta uno de los vértices. Dicha recta medirá 6,7 centímetros y se moverá hasta el lado inicial del cuadrado, el cual pasa convertirse en un rectángulo cuyos lados miden 9,7 y 6 centímetros. Al dividirse dichos valores se obtendrá el número phi, tal como se muestra en la imagen.

Demostración del rectángulo áureo

Por lo tanto, al momento de querer hacer un rectángulo áureo, conociendo la longitud de su lado menor, es decir, la altura del mismo, solo hay que multiplicar dicho valor por el del numero phi para hallar su lado menor, o lo que es lo mismo, su base, y si se sabe cuanto mide su lado mayor, o sea la base de rectángulo, solo hay que dividir este valor entre el del numero phi para saber cuanto valdrá su lado menor o altura, tal como se muestra en este ejemplo:

Como se calcula un rectángulo áureo

Una propiedad de los rectángulos áureos es que cuando se colocan dos iguales tal como se muestra en la figura, si se traza una diagonal desde la esquina inferior hasta la superior del conjunto, dicha diagonal pasa por tres vértices.

Propiedad del rectángulo áureo

El rectángulo áureo tiene gran uso en el arte y la arquitectura. Como se dijo anteriormente se le usaba en la Antigua Grecia en el diseño de sus edificaciones como el Partenon. Asimismo se le usa también en el diseño industrial, como por ejemplo las cajas de cigarros, carnets de identidad o las tarjetas de crédito.

Ejemplo del uso del rectángulo áureo

El numero áureo en geometría. Caso del pentágono y el pentagrama

Si se tiene un pentágono de vértices ABCDE. Si se traza una recta desde el vértice B hasta el vértice D, al dividir la distancia de dicha recta entre la del lado AB, da como resultado el numero phi. Lo mismo ocurre si se traza otra recta, esta vez entre los vértices E y C y se divide la distancia de la misma entre la del lado AE.

El numero áureo en el pentágono

Si se trazan otra recta esta vez entre los vértices B y E, otra entre los vértices A y D y entre los vértices A y C se obtiene una figura llamada pentagrama, en la cual también está presente en las proporciones de sus lados el número áureo, tal como se explica en la figura.

Pentagrama y número phi

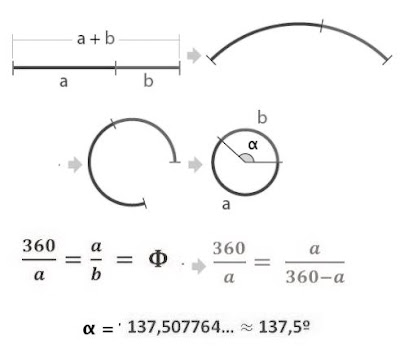
El ángulo de oro o áureo

Es la relación angular de proporción igual al numero phi entre dos segmentos que se les ha dado forma curva hasta formar un circulo. Este angulo se calcula tal como se muestra en la figura:

Angulo de oro

El angulo de oro está presente en la naturaleza. En el crecimiento de algunas plantas, las hojas deben disponerse, alrededor del tallo, de manera que reciban la máxima cantidad de luz solar. Si creciesen unas encima de las otras, la hoja de arriba impediría que la luz solar llegase a la hoja de abajo. Curiosamente, el ángulo que maximiza la cantidad de luz solar que reciben las hojas y que éstas no se tapen unas con otras es el ángulo de oro de 137,5º.

Relación entre el número phi y la serie de Fibonacci

Serie de Fibonacci

Descubierta por el matemático italiano Leonardo de Pisa, también conocido como Fibonacci. Esta serie es una sucesión de números naturales en la que los dos primeros números de la sucesión son 0 y 1 y los términos restantes son la suma de los 2 términos anteriores, tal como se muestra:

Primer termino: 0

Segundo termino: 1

Tercer termino: Se suman el primer y segundo termino

0 + 1 = 1

Cuarto termino: Se suman el segundo y tercer termino.

1 + 1 = 2

Quinto termino: Se suman el cuarto y tercer termino

1 + 2 = 3

Sexto termino: Se suman el cuarto y quinto termino.

3 + 2 = 5

y así sucesivamente, por lo que la serie de Fibonacci es de esta forma:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610,...

Esta serie es infinita.

Ahora bien, Si a partir del segundo termino dividimos dos términos consecutivos de la sucesión de Fibonacci, obtendremos un valor aproximado al número phi tal como se muestra a continuación:

2/1 =2

3/2 = 1,5

5/3 = 1,66667

8/5 = 1,6

13/8 = 1,625

21/13 = 1,61538

34/21 = 1,61904

55/34 = 1,61764

89/55 = 1,61818

144/89 = 1,61797

233/144 = 1,61805

377/233 = 1,61802

610/377 = 1,61803

Si se llama F_n a un numero de la serie de Fibonacci y F_n+1 al numero siguiente, el numero phi se expresa así:

Otra forma de expresar al número phi

Ahora vamos a suponer que tenemos un rectángulo cuyos lados tienen como valor dos términos consecutivos de la serie de Fibonacci y digamos que el lado mayor o base mide 21 unidades y el lado menor o altura mide 13 unidades. Como vimos anteriormente, si dividimos estos números obtendremos un valor aproximado al número phi. Ahora dividimos la base o lado mayor en dos partes, una que mida 13 unidades y la otra 8, siendo 13 y 8 dos términos consecutivos de la serie de Fibonacci, luego se divide la altura o lado menor en dos partes, una de 5 y otra de 8 unidades, y se sigue dividiendo hasta obtener una serie de cuadrados, tal como se muestra en la figura, indicándose la longitud de los lados de cada uno de estos, siendo la mismas números incluidos en la serie de Fibonacci

División de un rectángulo áureo en varios cuadros con medidas iguales a términos de la serie de Fibonacci

Si se traza una curva que una los vértices de uno de los cuadrados mas pequeños y dicha curva se va estirando, pasando por los vértices tal como se muestra en la figura se obtendrá la famosa espiral dorada o espiral de Fibonacci.

Espiral dorada o de Fibonacci

La espiral dorada es usada tanto en arte, arquitectura y diseño industrial y está presente también en la naturaleza.

La espiral dorada esta presente en el diseño y en la naturaleza

El numero áureo está muchas partes incluyendo el cuerpo humano, ya que al dividir la distancia entre el ombligo y la planta de los pies de una persona con la de su altura total da como resultado este número algo que se ve en el #Hombre de Vitruvio” pintado por Leonardo Da Vinci.

En el "Hombre de Vitruvio" se muestra la presencia del numero phi en el cuerpo humano

El numero áureo o phi es de gran importancia y esto solo fue un resumen del mismo. bueno vamos a dejarlo hasta aquí. Espero que haya sido de su agrado, si tienen algún comentario pueden hacerlo, igual que cualquier duda o sugerencia. ¡Hasta la próxima!